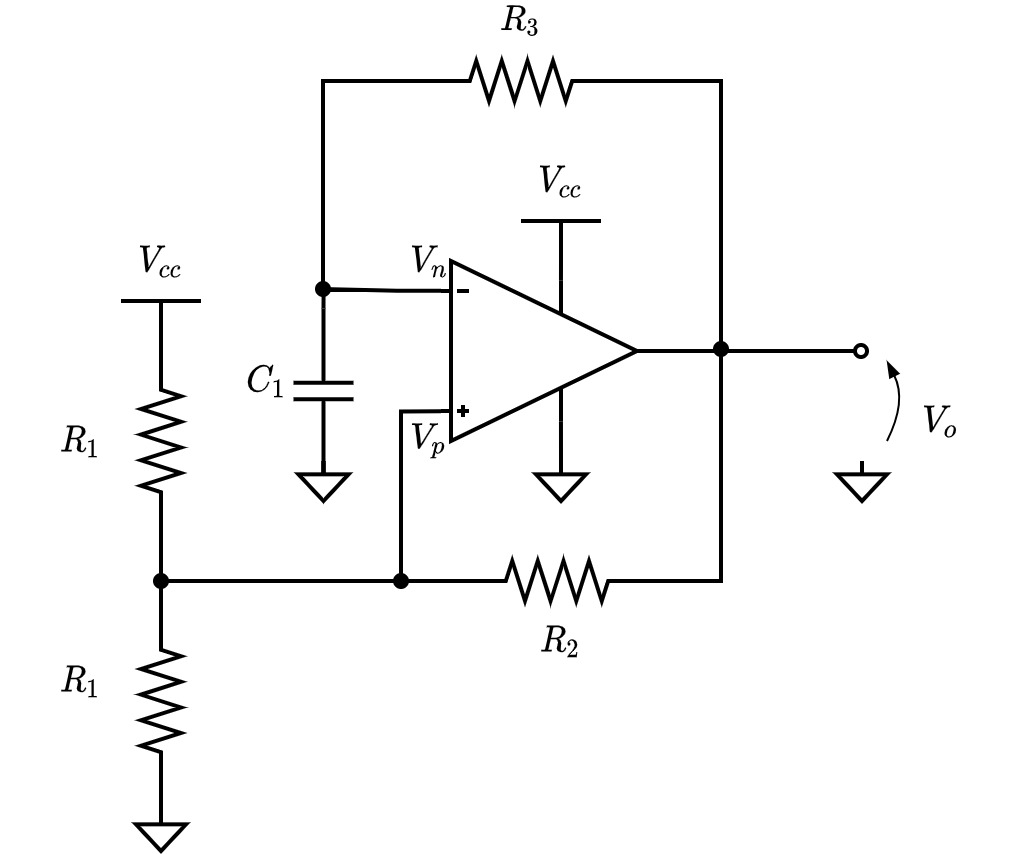
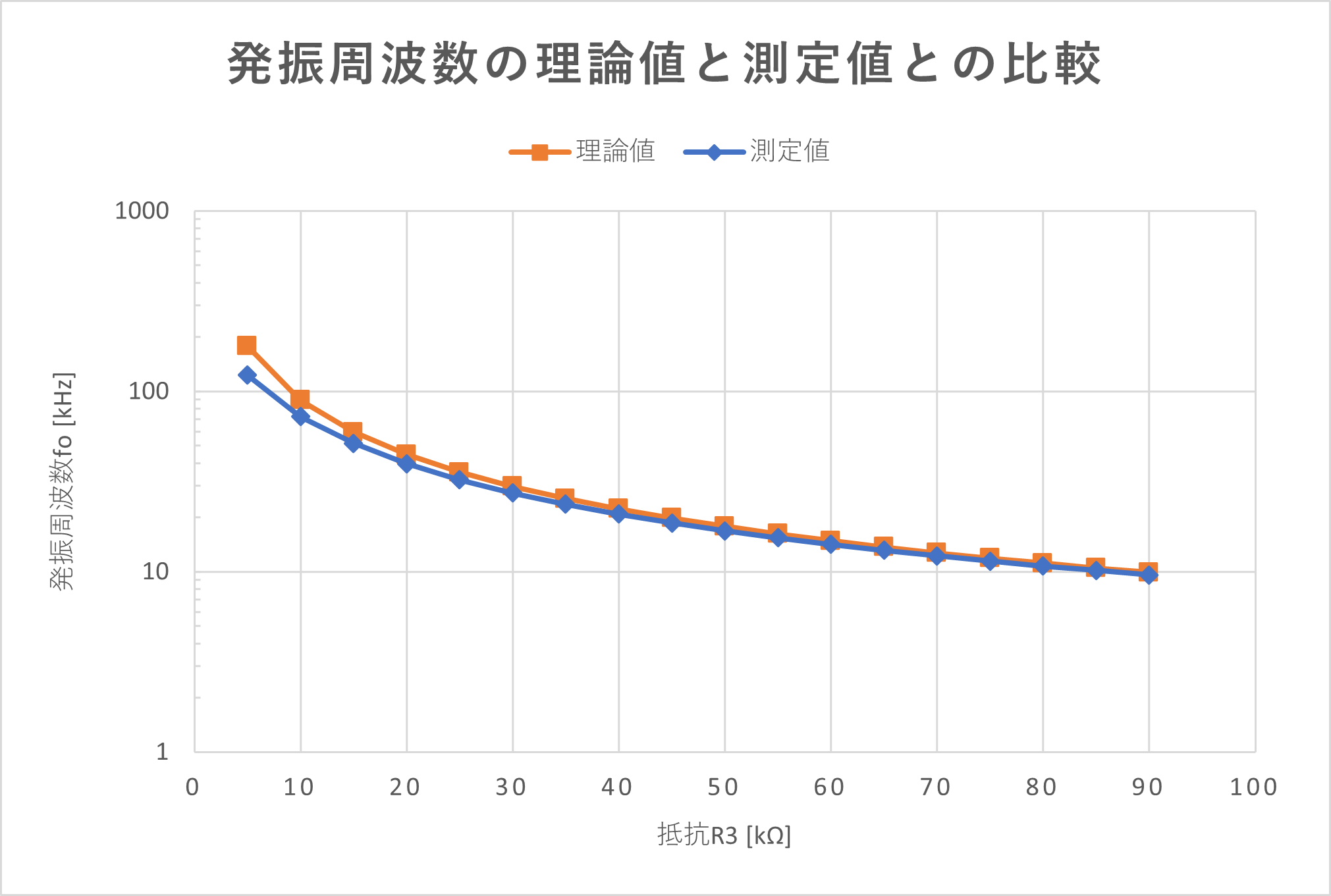
本節では, 発振周波数$f_o$を数式を用いて導出します. 回路図Fig.1. をナレータ・ノレータモデルを用いて書き直すと, Fig.4. になります.
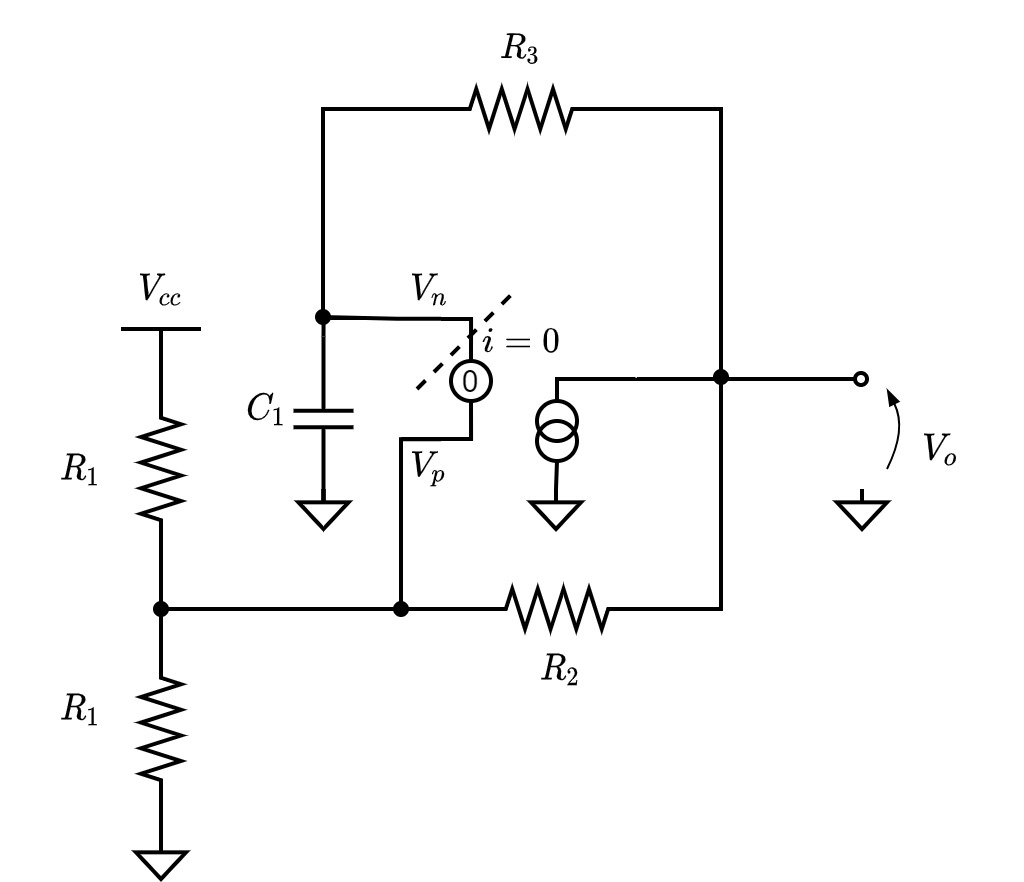Fig.4. ナレータ・ノレータモデルで書き直した回路図. 仮想短絡でないと仮定すると, 破線部で回路を切ることができる. オペアンプ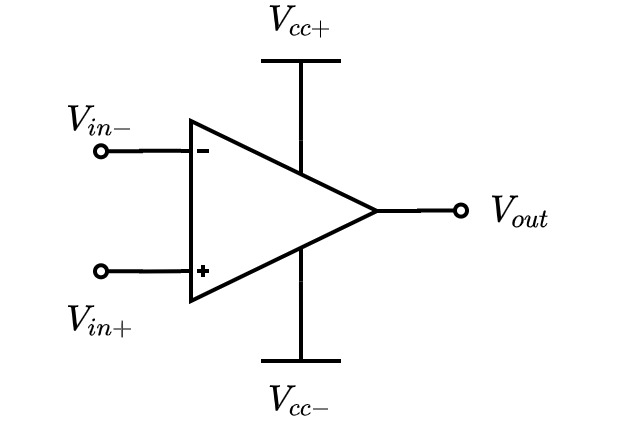
Fig.5. オペアンプ回路図オペアンプの動作を表す式は, 以下のようになります. ただし, $A_V$は, 増幅率で, 理想オペアンプの場合, $A_V=\infty$になります.
$$
\begin{equation*}
V_{out} = A_V (V_{in+} - V_{in-})
\end{equation*}
$$
出力電圧$V_{out}$について, 理想オペアンプの場合, $-\infty < V_{out} < +\infty$ ですが, 実際は, 正負電源電圧間 $V_{cc-} < V_{out} < V_{cc+}$に制限されます.
ナレータ・ノレータモデル
理想オペアンプは, 多くの場合, 二つの変わった素子(ナレータとノレータ)によってモデル化されます. 理想オペアンプの等価回路を, Fig.6. に示します.
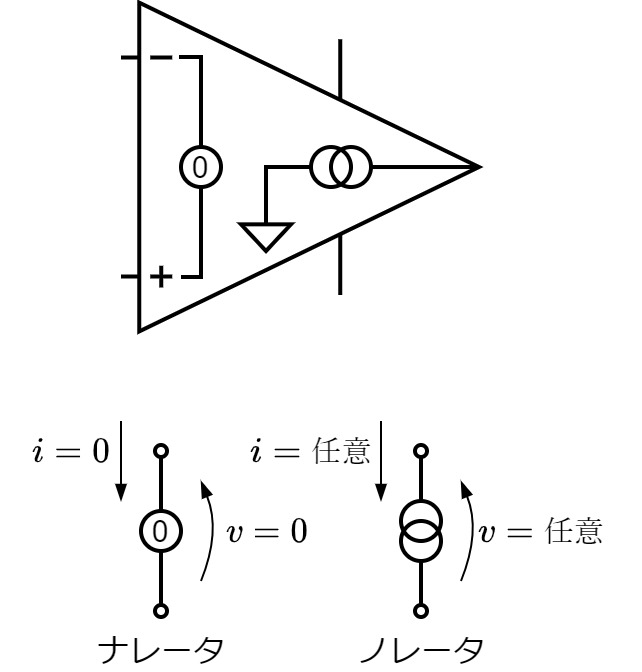Fig.6. 理想オペアンプ等価回路ナレータは, 両端子間で電流を通さず, 等電位です. ノレータは, 任意の電流と電圧を設定できます.
ナレータの両端子間が等電位であることを, 仮想短絡(Virtual Short)と呼びます. ただしこの条件は, すべての場合で使えるとは限らないことに注意してください(本稿では, この条件を仮定においていません).
回路図Fig.4. において, 仮想短絡を仮定しないとすると, 破線部で回路を二つに分けることができます. オペアンプの正入力端子側と負入力端子側それぞれの回路図を以下に示します.
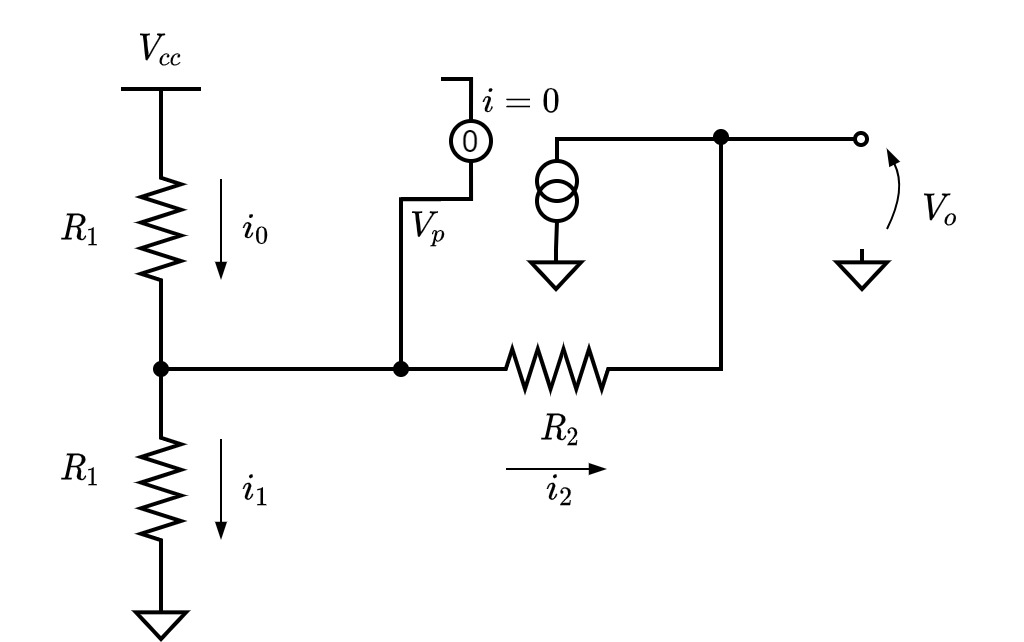Fig.7. 正入力端子側の回路図
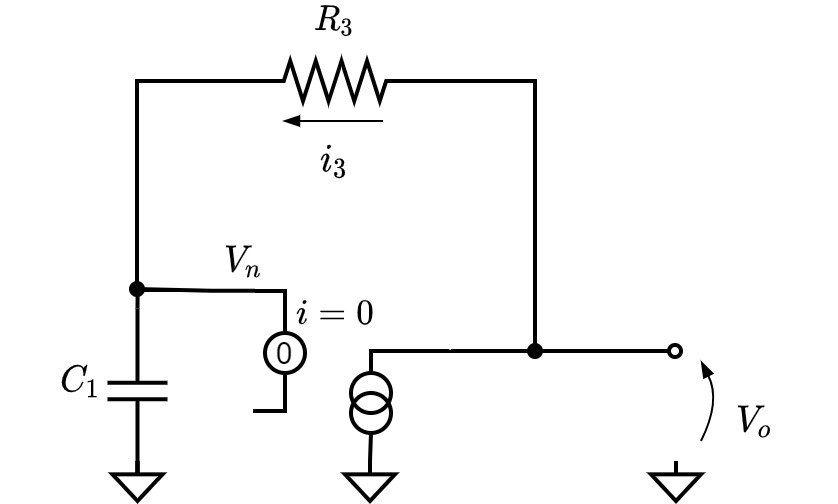Fig.8. 負入力端子側の回路図正入力端子側の回路図Fig.7. に注目して, $V_p$について解きます. キルヒホッフの第一, 第二法則から, 以下の関係式を得ます.
$$
\begin{align}
& i_0 = i_1 + i_2 \label{eq:1} \\
& V_{cc} - R_1 i_0 = V_p \label{eq:2} \\
& R_1 i_1 = V_p \label{eq:3} \\
& V_p -R_2 i_2 = V_o \label{eq:4}
\end{align}
$$
式(\ref{eq:1})から, $i_0$について解くと,
$$
\begin{align}
i_0 &= i_1 + i_2 \nonumber \\
&= \frac{V_p}{R_1} + i_2 \quad &((\ref{eq:3})より) \nonumber \\
&= \frac{V_p}{R_1} + (V_p - V_o) \frac{1}{R_2} \quad &((\ref{eq:4})より) \label{eq:5}
\end{align}
$$
式(\ref{eq:2})から, $V_p$について解くと,
$$
\begin{align}
V_{cc} - R_1 i_0 &= V_p \nonumber \\
V_{cc} - V_p - \frac{R_1}{R_2}(V_p - V_o) &= V_p \quad ((\ref{eq:5})より) \nonumber \\
V_p &= \frac{R_1 V_o}{R_1 + 2 R_2} + \frac{R_2 V_{cc}}{R_1 + 2 R_2} \label{eq:6}
\end{align}
$$
以上から, $V_p$について解くことができました.
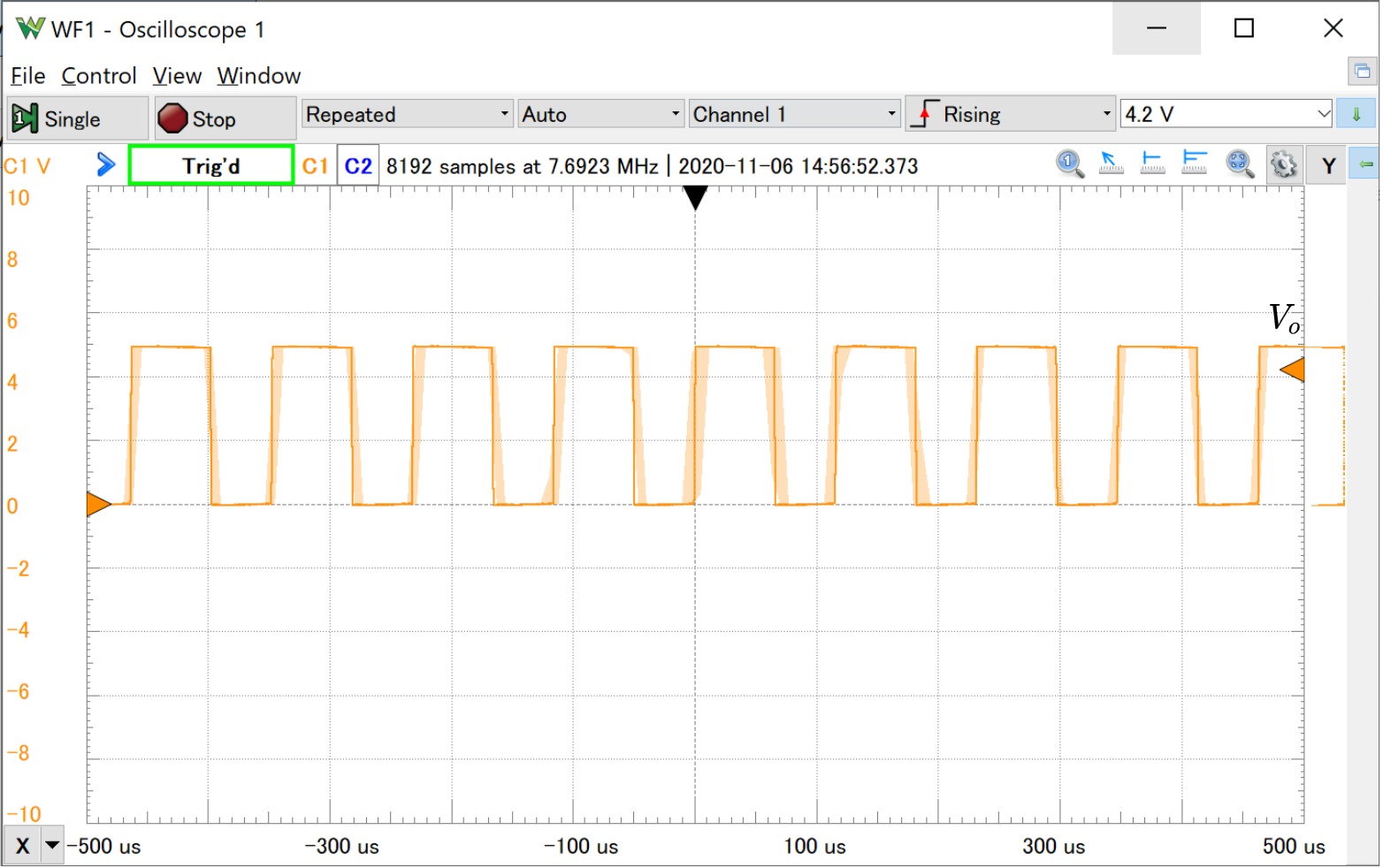
次に, Fig.3. 内にある発振中の各時刻$t_1, t_2, t_3$について考えます.
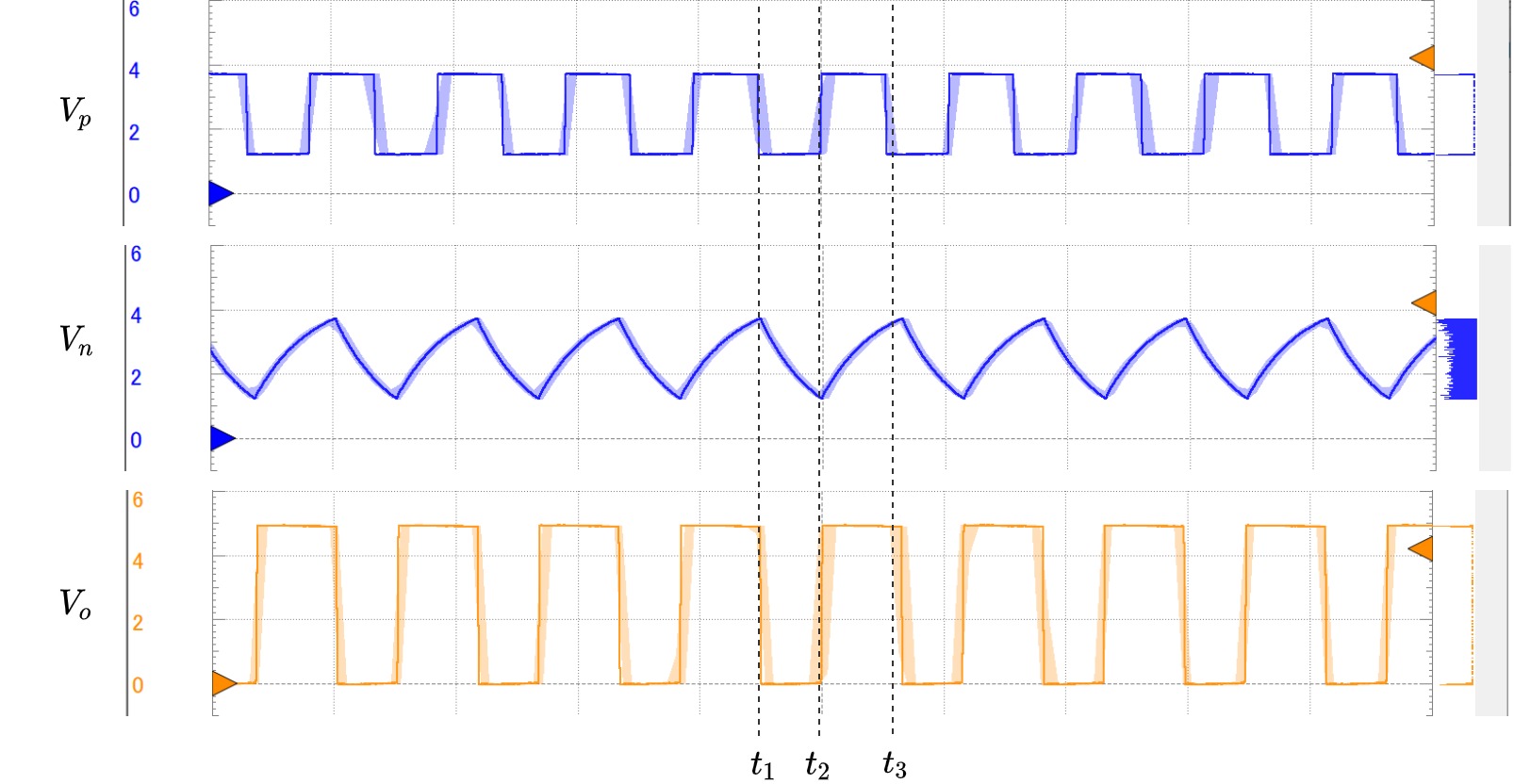Fig.3. 発振中の各電位の変化. 時刻$t_1$で, $V_n$が$V_p$に追い付き, $V_o$が0Vになり, 時刻$t_2$で, $V_n$が$V_p$まで落ち, $V_o$が5Vになっていることが分かる. 時刻$t_1$において, $V_n$が$V_p$に追い付いたとき, 以下の関係式を得ることができます. ただし, $V_{p, t_1}, V_{n,t_1}$はそれぞれ, 時刻$t_1$での$V_p, V_n$を表すとします.
$$
\begin{align}
V_{p,t_1} &= \frac{R_1 + R_2}{R_1 + 2 R_2}V_{cc} \quad ((\ref{eq:6}), V_o=V_{cc}より) \label{eq:7} \\
V_{n,t_1} &= V_{p,t_1} \label{eq:8}
\end{align}
$$
時刻$t_2$において, $V_n$が$V_p$まで落ちたとき, 以下の関係式を得ることができます. ただし, $V_{p, t_2}, V_{n,t_2}$はそれぞれ, 時刻$t_2$での$V_p, V_n$を表すとします.
$$
\begin{align}
V_{p,t_2} &= \frac{R_2}{R_1 + 2 R_2}V_{cc} \quad ((\ref{eq:6}), V_o=0より) \label{eq:9} \\
V_{n,t_2} &= V_{p,t_2} \label{eq:10}
\end{align}
$$
時刻$t_3$において, 再び$V_n$が$V_p$に追い付いたとき, 以下の関係式を得ることができます. ただし, $V_{p, t_3}, V_{n,t_3}$はそれぞれ, 時刻$t_3$での$V_p, V_n$を表すとします.
$$
\begin{align}
V_{p,t_3} &= \frac{R_1 + R_2}{R_1 + 2R_2} V_{cc} \quad ((\ref{eq:6}), V_o=V_{cc}より) \label{eq:11} \\
V_{n,t_3} &= V_{p,t_3} \label{eq:12}
\end{align}
$$
次に, 時刻$t_1, t_2, t_3$の関係式を得るために, $t_1$ ~ $t_2$間と, $t_2$ ~ $t_3$間について考えます.
$t_1$ ~ $t_2$間で, $V_n$が$V_p$まで落ちた(Fig.3. を参照)つまり, コンデンサ$C_1$が放電したことを意味するので, 負入力端子側の回路図Fig.8. を書き直すと以下のようになります.
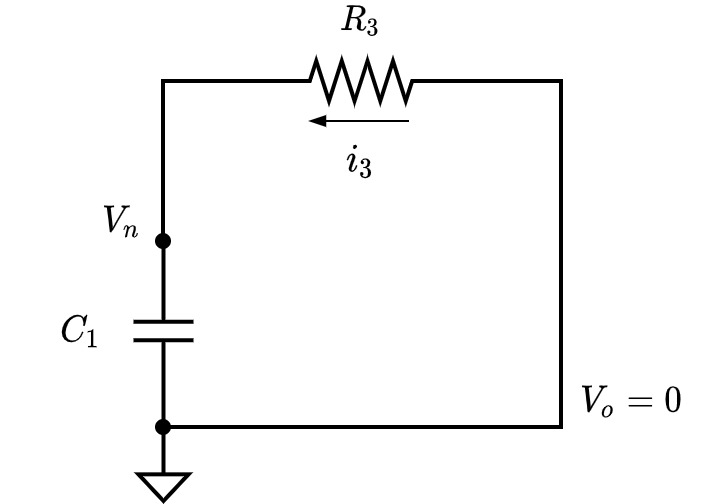Fig.9. 放電時の回路図キルヒホッフの第一, 第二法則から以下の関係式を得ます.
$$
\begin{align}
& i_3 = C_1 \frac{dV_n}{dt} \label{eq:13} \\
& V_n + R_3 i_3 = 0 \label{eq:14}
\end{align}
$$
コンデンサ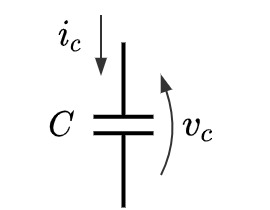
Fig.10. コンデンサ回路図コンデンサの動作を表す式は以下の通りです. $v_c$の向きの取り方で$i_c$の向きが決まることに注意してください.
$$
\begin{equation*}
i_c = C \frac{dv_c}{dt}
\end{equation*}
$$
- 導出)
$$
\begin{align*}
q &= C v_c \\
\frac{dq}{dt} &= C \frac{d v_c}{dt} \\
i_c &= C \frac{d v_c}{dt} \quad (i_c = \frac{dq}{dt} より)
\end{align*}
$$
式(\ref{eq:14})から, $V_n$について解くと,
$$
\begin{align}
V_n &= - R_3 i_3 \nonumber \\
V_n &= - R_3 C_1 \frac{dV_n}{dt} \quad ((\ref{eq:13})より) \nonumber \\
\frac{dV_n}{dt} &= -\frac{V_n}{R_3 C_1} \nonumber \\
\int \frac{1}{V_n} \frac{dV_n}{dt} dt &= \int - \frac{1}{R_3 C_1} dt \nonumber \\
\ln |V_n| &= -\frac{t}{R_3 C_1} + K \quad (Kは積分定数) \nonumber \\
V_n &= \pm \exp(K) \exp(-\frac{t}{R_3 C_1}) \nonumber \\
V_n &= A \exp(-\frac{t}{R_3 C_1}) \quad (A=\pm \exp(K) とおく) \label{eq:15}
\end{align}
$$
初期条件, 時刻$t_1$で, $V_n=V_{n,t_1}$であることから, $A$について解くと,
$$
\begin{align}
V_{n,t_1} &= A \exp(-\frac{t_1}{R_3 C_1}) \nonumber \\
\frac{R_1 + R_2}{R_1 + 2 R_2}V_{cc} &= A \exp(-\frac{t_1}{R_3 C_1}) \quad ((\ref{eq:7}), (\ref{eq:8})より) \nonumber \\
A &= \frac{R_1 + R_2}{R_1 + 2 R_2}V_{cc} \exp(\frac{t_1}{R_3 C_1}) \label{eq:16}
\end{align}
$$
時刻$t_2$で, $V_n=V_{n,t_2}$であることから, 式(\ref{eq:15})に代入して,
$$
\begin{align}
V_{n,t_2} &= A \exp(-\frac{t_2}{R_3 C_1}) \nonumber \\
\frac{R_2}{R_1 + 2R_2} V_{cc} &= A \exp(-\frac{t_2}{R_3 C_1}) \quad ((\ref{eq:9}), (\ref{eq:10})より) \nonumber \\
\frac{R_2}{R_1 + 2R_2} V_{cc} &= \frac{R_1 + R_2}{R_1 + 2 R_2}V_{cc} \exp(\frac{t_1}{R_3 C_1}) \exp(-\frac{t_2}{R_3 C_1}) \quad ((\ref{eq:16})より) \nonumber \\
\exp(\frac{t_2 - t_1}{R_3 C_1}) &= \frac{R_1 + R_2}{R_2} \nonumber \\
\frac{t_2 - t_1}{R_3 C_1} &= \ln \frac{R_1 + R_2}{R_2} \nonumber \\
t_2 - t_1 &= R_3 C_1 \ln \frac{R_1 + R_2}{R_2} \label{eq:17}
\end{align}
$$
以上から, $t_1, t_2$の関係式を得ました.
$t_2$ ~ $t_3$間で, $V_n$が$V_p$まで追いついた(Fig.3. を参照)つまり, コンデンサ$C_1$が充電したことを意味するので, 負入力端子側の回路図Fig.8. を書き直すと以下のようになります.
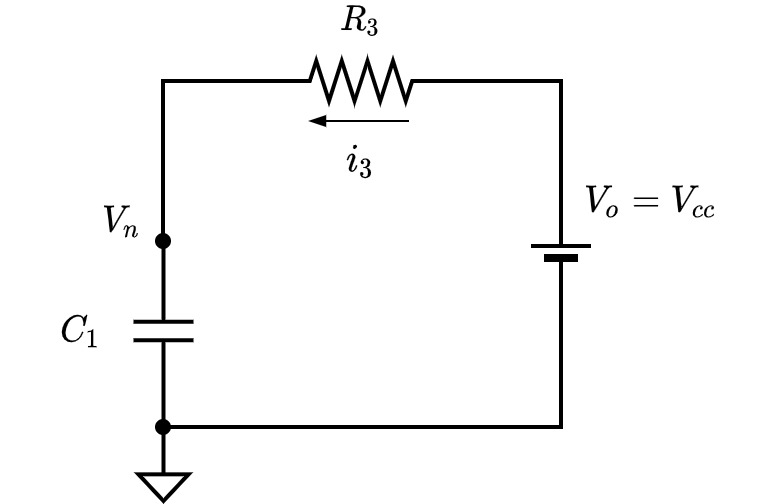Fig.11. 充電時の回路図キルヒホッフの第一, 第二法則から以下の関係式を得ます.
$$
\begin{align}
& i_3 = C_1 \frac{dV_n}{dt} \label{eq:18} \\
& V_{cc} - R_3 i_3 = V_n \label{eq:19}
\end{align}
$$
式(\ref{eq:19})から, $V_n$について解くと,
$$
\begin{align}
V_{cc} - R_3 i_3 &= V_n \nonumber \\
V_{cc} - R_3 C_1 \frac{dV_n}{dt} &= V_n \quad ((\ref{eq:18})より) \nonumber \\
R_3 C_1 \frac{dV_n}{dt} &= V_{cc} - V_n \nonumber \\
\frac{1}{V_{cc} - V_n} \frac{dV_n}{dt} &= \frac{1}{R_3 C_1} \nonumber \\
\int \frac{1}{V_{cc} - V_n} \frac{dV_n}{dt} dt &= \int \frac{1}{R_3 C_1} dt \nonumber \\
\ln |V_{cc} - V_n| &= -\frac{t}{R_3 C_1} + K \quad (Kは積分定数) \nonumber \\
V_{cc} - V_n &= \pm \exp(K) \exp(-\frac{t}{R_3 C_1}) \nonumber \\
V_{cc} - V_n &= A \exp(-\frac{t}{R_3 C_1}) \quad (A=\pm \exp(K) とおく) \nonumber \\
V_n &= V_{cc} - A \exp(-\frac{t}{R_3 C_1}) \label{eq:20}
\end{align}
$$
初期条件, 時刻$t_2$で, $V_n=V_{n,t_2}$であることから, $A$について解くと,
$$
\begin{align}
V_{n,t_2} &= V_{cc} - A \exp(-\frac{t_2}{R_3 C_1}) \nonumber \\
\frac{R_2}{R_1 + 2R_2}V_{cc} &= V_{cc} - A \exp(-\frac{t_2}{R_3 C_1}) \quad ((\ref{eq:9})(\ref{eq:10})より) \nonumber \\
A &= \frac{R_1 + R_2}{R_1 + 2R_2} V_{cc} \exp(\frac{t_2}{R_3 C_1}) \label{eq:21}
\end{align}
$$
時刻$t_3$で, $V_n=V_{n,t_3}$であることから, 式(\ref{eq:20})に代入して,
$$
\begin{align}
V_{n,t_3} &= V_{cc} - A \exp(-\frac{t_3}{R_3 C_1}) \nonumber \\
\frac{R_1 + R_2}{R_1 + 2R_2} V_{cc} &= V_{cc} - A \exp(-\frac{t_3}{R_3 C_1}) \quad ((\ref{eq:11})(\ref{eq:12})より) \nonumber \\
\frac{R_1 + R_2}{R_1 + 2R_2} V_{cc} &= V_{cc} - \frac{R_1 + R_2}{R_1 + 2R_2} V_{cc} \exp(\frac{t_2}{R_3 C_1}) \exp(-\frac{t_3}{R_3 C_1}) \nonumber \\
\exp(\frac{t_3 - t_2}{R_3 C_1}) &= \frac{R_1 + R_2}{R_2} \nonumber \\
\frac{t_3 - t_2}{R_3 C_1} &= \ln \frac{R_1 + R_2}{R_2} \nonumber \\
t_3 - t_2 &= R_3 C_1 \ln \frac{R_1 + R_2}{R_2} \label{eq:22}
\end{align}
$$
以上から, $t_2, t_3$の関係式を得ました.
最後に, 発振周期$T_o$について, $T_o=t_3 - t_1$より,
$$
\begin{align}
T_o &= t_3 - t_1 \nonumber \\
&= (t_3 - t_2) + (t_2 - t_1) \nonumber \\
&= R_3 C_1 \ln \frac{R_1 + R_2}{R_2} + R_3 C_1 \ln \frac{R_1 + R_2}{R_2} \quad ((\ref{eq:17}), (\ref{eq:22})より) \nonumber \\
&= 2 R_3 C_1 \ln \frac{R_1 + R_2}{R_2} \label{eq:23}
\end{align}
$$
よって, 発振周波数$f_o=1/T_o$は,
$$
\begin{align}
f_o &= \frac{1}{T_o} \nonumber \\
&= \frac{1}{2 R_3 C_1 \ln \frac{R_1 + R_2}{R_2}} \quad ((\ref{eq:23})より) \nonumber \\
&= \frac{1}{2 R_3 C_1 \ln \left(1 + \frac{R_1}{R_2}\right) } \label{eq:24}
\end{align}
$$
