図で理解する変換行列と表現行列

公開日: 2019-11-26

更新日: 2023-08-07

線形代数にある線形写像, 基底の変換行列, 表現行列などを理解するとき, 今どこの座標系にいるのか, 基底は変わったのか, ここはベクトル空間かという悩みに会います.

本稿では, 変換行列や表現行列を図で理解することを目的にします. 行列の掛け算が点の移動であることを意識すると, 理解しやすくなります.

ベクトル空間

空でない集合$V$に, 和および スカラー倍 が定義されているとき, $V$を ベクトル空間, $V$の要素を ベクトルといいます. すなわち,

(i) $a, b \in V$に対して, $a+b\in V$
(ii) $a\in V$ と $k \in K$ に対して, $ka \in V$

が定義されているとき$V$をベクトル空間といいます.

(注): $K$が実数体のとき $V$ を実ベクトル空間, $K$が複素数体のとき$V$を複素ベクトル空間といいます.

数ベクトル空間

$n$次の列ベクトル$x={}^t\!(x_1 x_2 \ldots x_n)$の全体からなるベクトル空間を$n$次元数ベクトル空間といい, その要素$x$を数ベクトルといいます.

特に, $x_n$が実数のとき, 数ベクトル空間は実$n$次元数空間 $R^n$ といいます.

線形写像

$V$, $W$を$K$上のベクトル空間とします．写像$f: V \rightarrow W$が次の(i), (ii)を満たすとき$V$から$W$への線形写像といいます．

(i) $f(a + b)=f(a) + f(b) \quad (a, b \in V)$
(ii) $f(ka) = kf(a) \quad (a \in V, k \in K)$

特に $V=W$のとき，線形変換(一次変換)といいます．

図で考えていきましょう.

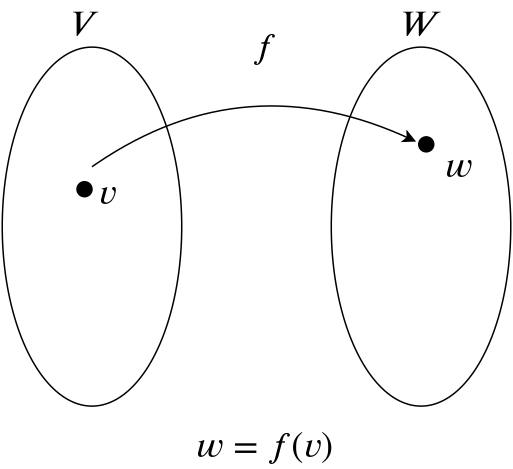
写像$f$によって，点$v(\in V)$を点$w(\in W)$移すとき，次の式で表せます．

$$w = f(v)$$

図で表すと次のようになります．

また，$V=R^n, W=R^m$とするとき，$f$は行列$A(m \times n)$で表せます．

$$w = Av $$

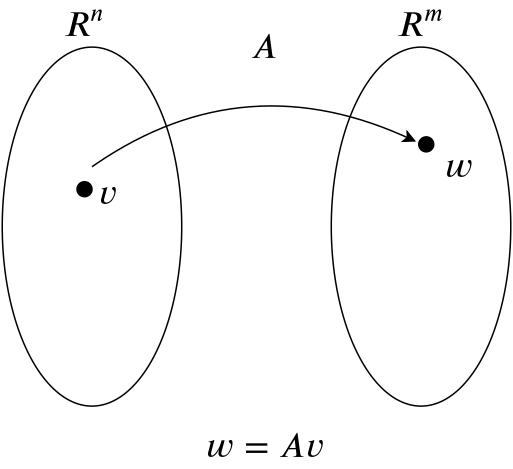
以上からわかるように, 移動元の点$v$の左から写像$A$をかけることで, 移動先である点$w$に移ります.

座標

$v$をベクトル空間$V$の任意のベクトルとし, ${\phi_1, \phi_2, \ldots, \phi_n}$を$V$の基底とします. このとき, $v$は, 以下のように$\phi_1, \phi_2, \ldots , \phi_n$の一次結合で一意的にあらわされます.

\begin{eqnarray} v=x_1 \phi_1 + x_2 \phi_2 + \ldots + x_n \phi_n \label{eq:v} \end{eqnarray}

$x={}^t\!(x_1 x_2 \ldots x_n)$を, 基底${\phi_1, \phi_2, \ldots, \phi_n}$ に関する$v$の座標といいます.

図で考えていきましょう.

$\phi_1, \phi_2, \ldots , \phi_n$ を横に並べたものを新しく行列$\phi = (\phi_1 \phi_2 \ldots \phi_n)$としたとき式(\ref{eq:v}) は次のように変形できます.

\begin{eqnarray} v &=& x_1 \phi_1 + x_2 \phi_2 + \ldots + x_n \phi_n \nonumber \\ &=& (\phi_1 \phi_2 \ldots \phi_n) \left( \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right) \nonumber \\ &=& \phi x \nonumber \end{eqnarray}

このことから, $\phi$は, 座標$x$が属している数ベクトル空間$R^n$からベクトル$v$が属するベクトル空間$V$へ移す写像とみれます.

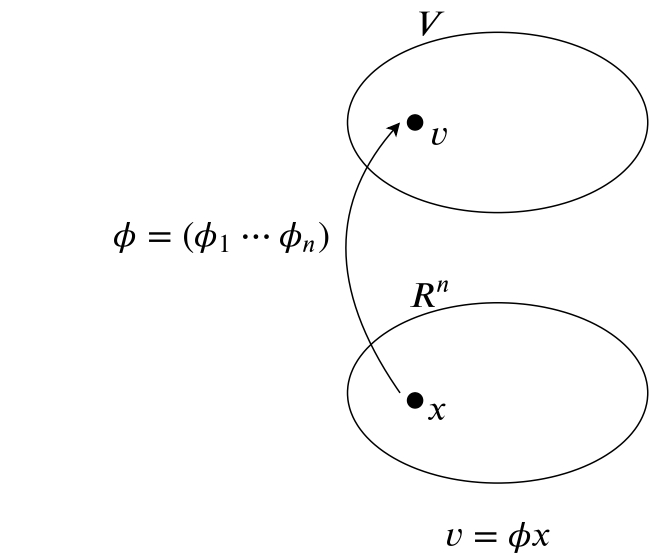
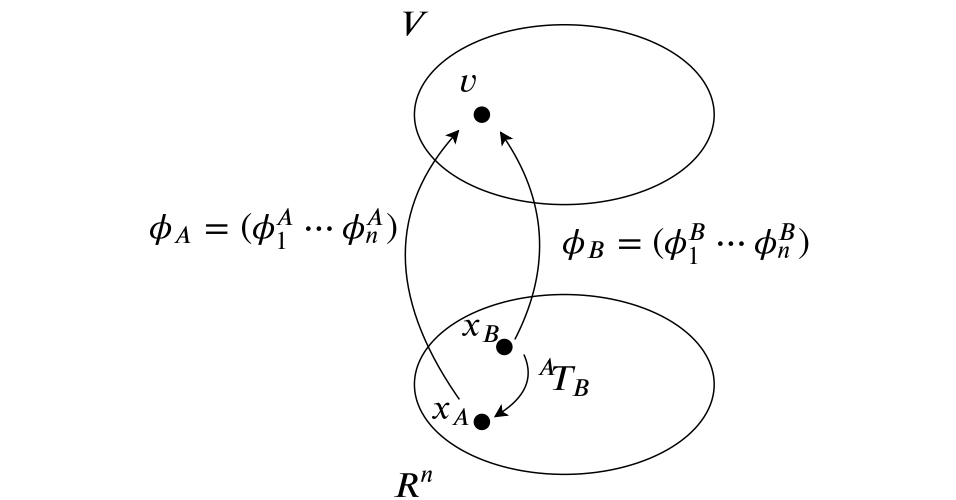
基底の変換行列

ベクトル空間$V$の二つの基底を $\Phi_A=\{\phi^A_1, \cdots , \phi^A_n\}$, $\Phi_B=\{\phi^B_1, \cdots , \phi^B_n\}$とします. $\Phi_A$から$\Phi_B$への基底の変換行列$P$は次のようになります(定義). ただし, $\phi_A = (\phi^A_1 \cdots \phi^A_n)$, $\phi_B = (\phi^B_1 \cdots \phi^B_n)$とします.

\begin{eqnarray} \phi_B = \phi_A P \label{eq:basis-trans} \end{eqnarray}

図で考えていきましょう.

今, ベクトル$v$に対して二つの基底$\Phi_A$, $\Phi_B$をとりました. 基底をいくつとろうが, 示しているのは一つのベクトル$v$です. ただ, 基底が二つあるので, 各基底ごとの座標(数ベクトル)は二つ現れます.

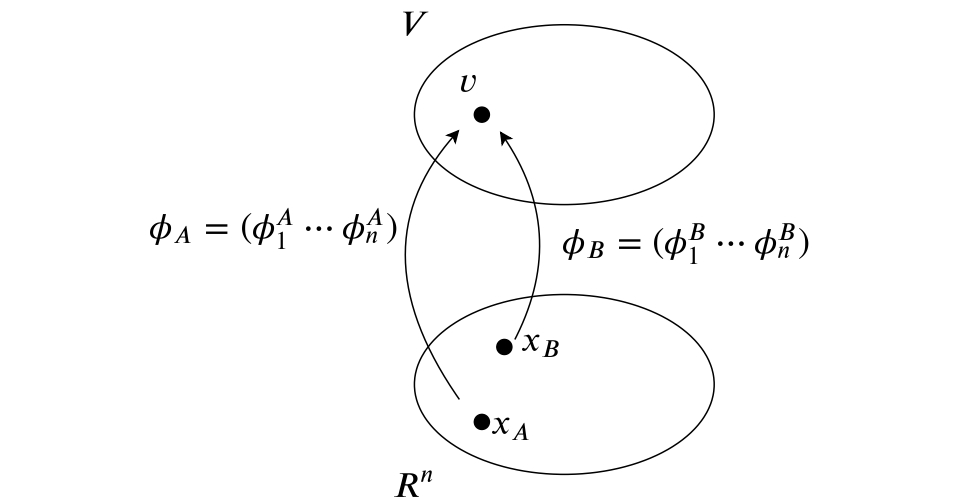
$v$について, 以下の二式が立てられます.

\begin{eqnarray} v = \phi_A x_A \nonumber \end{eqnarray} \begin{eqnarray} v = \phi_B x_B \nonumber \end{eqnarray}

よって,

\begin{eqnarray} \phi_A x_A &=& \phi_B x_B \nonumber \\ x_A &=& \phi_A^{-1} \phi_B x_B \nonumber \end{eqnarray}

ここで, 式(\ref{eq:basis-trans})から, $P=\phi_A^{-1}\phi_B$なので, 上式は次のようになります.

\begin{eqnarray} x_A = P x_B \nonumber \end{eqnarray}

上の式が意味するのは, 点$x_B$が行列$P$によって点$x_A$に移動することです. 図に入れるとこうなります.

同次変換行列

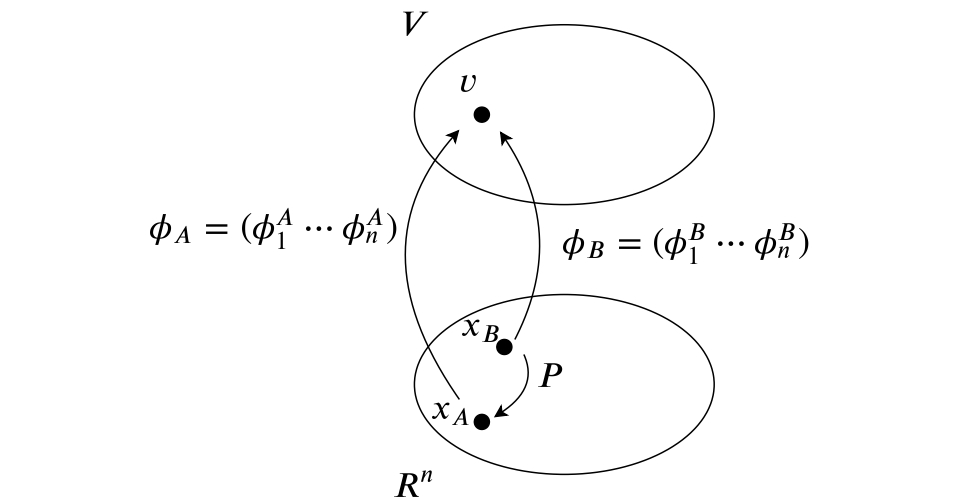
同次変換行列も同じ点に対して, 見ている座標系が違う意味で, 基底の変換行列の一種です.

点$x_B$を点$x_A$に移す変換行列${}^A\!T_B$があるとき, 図示すると次のようになります.

表現行列

$V$, $W$ を $\mathbb{F}$上の有限次元ベクトル空間とし, $f:V \rightarrow W$を線形写像とします. $V$, $W$の基底をそれぞれ$\Phi=\{\phi_1, \cdots , \phi_n\}$, $\Psi=\{\psi_1, \cdots , \psi_m\}$とします. このとき, 以下の式を満たす行列$A$を$V$の基底$\Phi$, $W$の基底$\Psi$に関する$f$の表現行列といいます(定義).

\begin{eqnarray} (f(\phi_1) \cdots f(\phi_n)) = (\psi_1 \cdots \psi_m)A \label{eq:rep} \end{eqnarray}

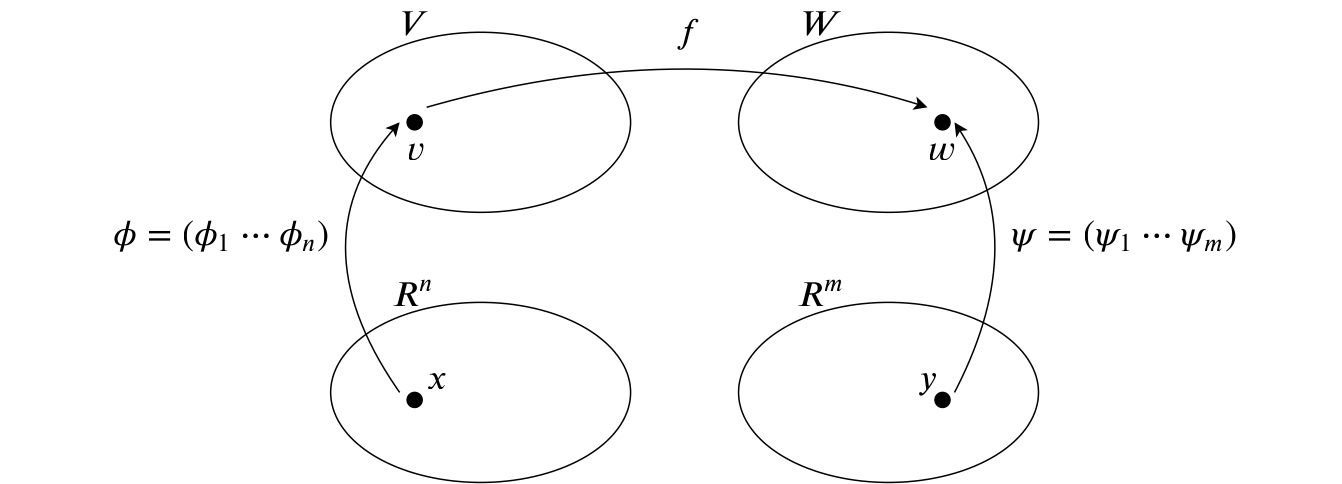
図で考えていきましょう.

ベクトル空間$V$上のある点$v$が, 写像$f$によってベクトル空間$W$上の点$w$に移るとしましょう. 基底$\Phi$に関する$v$の座標を$x$, 基底$\Psi$に関する$w$の座標を$y$とします.

今までの, 線形写像の図示, 基底の変換行列の図示を踏まえて, 図示してみましょう.

$y$が$\psi$で$w$に移されることから, $w=\psi y$が成り立ちます. 両辺に$\psi^{-1}$をかけて, $y=\psi^{-1} w$が成り立ちます. では, ここから右辺に$x$が出るまで, 展開していきます.

\begin{eqnarray} y &=& \psi^{-1} w \nonumber \\ &=& \psi^{-1} f(v) \quad (w = f(v) より) \nonumber \\ &=& \psi^{-1} f(\phi x) \quad (v = \phi x より) \nonumber \end{eqnarray}

次に$f(\phi x)$の内部を展開していきます.

\begin{eqnarray} y &=& \psi^{-1} f(\phi x) \nonumber \\ &=& \psi^{-1} f((\phi_1 \phi_2 \cdots \phi_n) \left( \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right)) \nonumber \\ &=& \psi^{-1} f(x_1 \phi_1 + x_2 \phi_2 + \cdots + x_n \phi_n) \nonumber \\ &=& \psi^{-1} (f(x_1 \phi_1) + f(x_2 \phi_2) + \cdots + f(x_n \phi_n)) \quad (fの線形性より) \nonumber \\ &=& \psi^{-1} (x_1 f(\phi_1) + x_2 f(\phi_2) + \cdots + x_n f(\phi_n)) \quad (fの線形性より) \nonumber \\ &=& \psi^{-1} ( f(\phi_1) f(\phi_2) \cdots f(\phi_n) ) \left( \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right) \nonumber \\ &=& \psi^{-1} (f(\phi_1) f(\phi_2) \cdots f(\phi_n)) x \label{eq:rep-sub-1} \end{eqnarray}

また, 表現行列の定義式(\ref{eq:rep})の両辺に$\psi^{-1}$をかけて, 次式を得ます.

\begin{eqnarray} A=\psi^{-1} (f(\phi_1) f(\phi_2) \cdots f(\phi_n)) \label{eq:rep-sub-2} \end{eqnarray}

式(\ref{eq:rep-sub-1}), 式(\ref{eq:rep-sub-2})から,

\begin{eqnarray} y=Ax \nonumber \end{eqnarray}

上の式が意味するのは, 点$x$が表現行列$A$で点$y$に移ることです. 図示すると次のようになるでしょう.

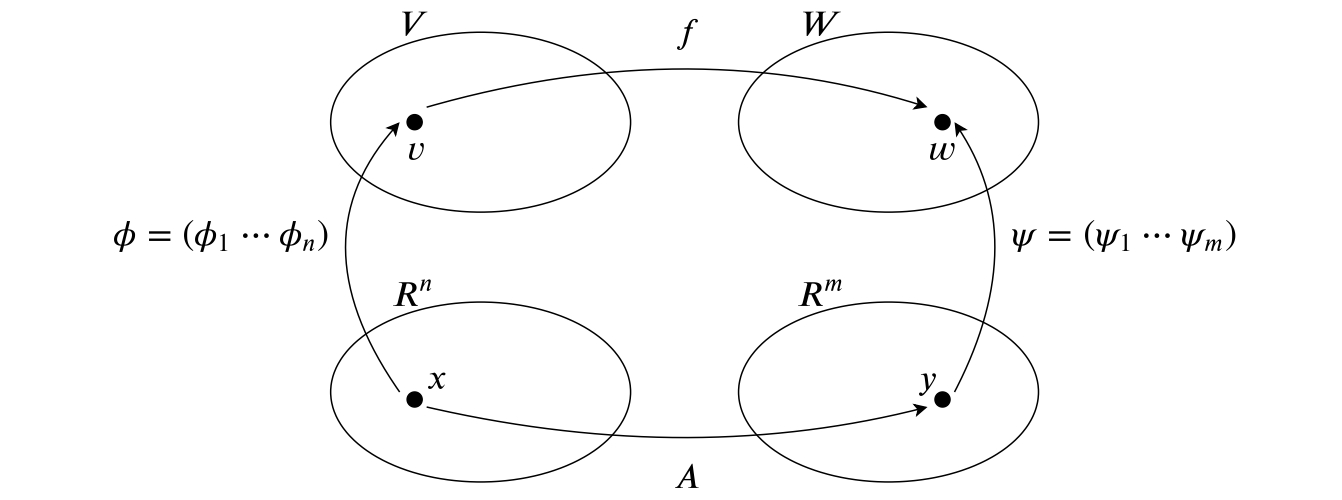
全体像

以上をまとめて, 図示してみましょう.

まとめ

基本的に上のような図が書ければ, そのほかの諸定理も比較的簡単に導けます.

諸定理

$f: V \rightarrow W$を線形写像とする. $f$の$V$の基底$\Phi_A = \{\phi^A_1, \cdots , \phi^A_n\}$, $W$の基底$\Psi_B = \{\psi^A_1, \cdots , \psi^A_m\}$ に関する表現行列を$A$, $f$の$V$の基底$\Phi_B = \{\phi^B_1, \cdots , \phi^B_n\}$, $W$の基底$\Psi_B = \{\psi^B_1, \cdots , \psi^B_m\}$ に関する表現行列を$B$とすると, $B=Q^{-1}AP$となる. ただし, $P$は$\Phi_A$から$\Phi_B$への基底の変換行列, $Q$は$\Psi_A$から$\Psi_B$への基底の変換行列とする.

もう一度全体像を見ます.

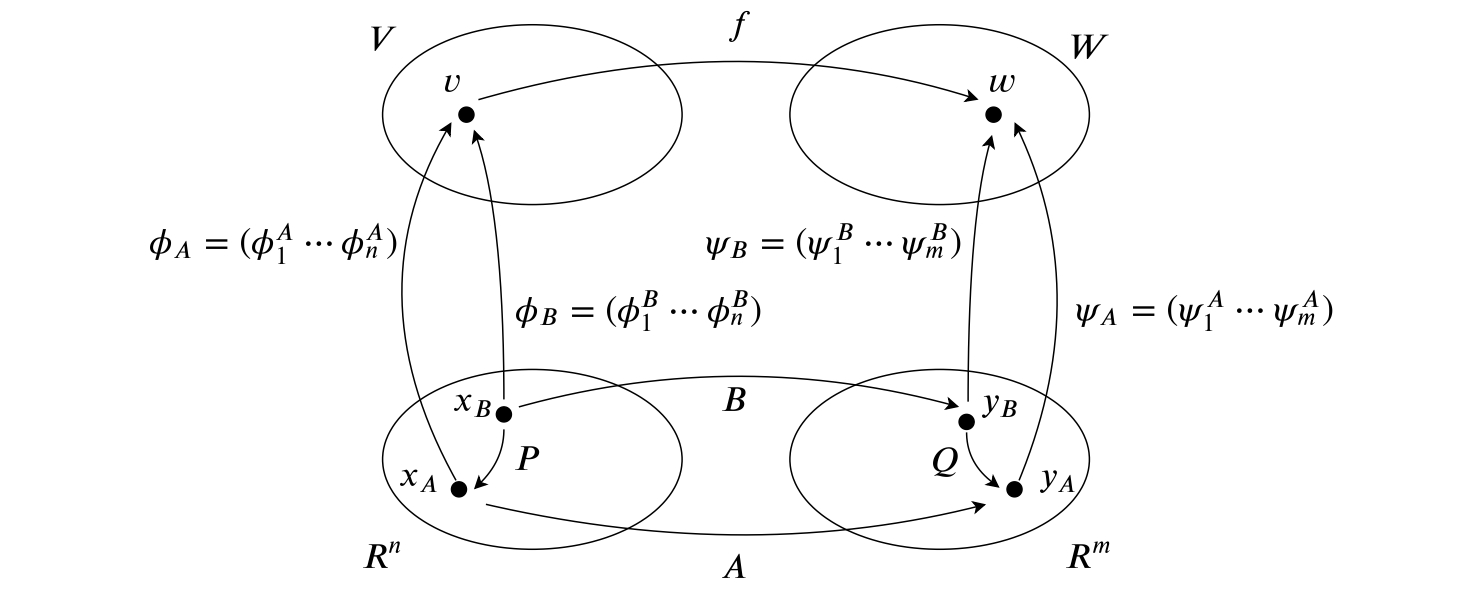
$x_B$から$y_B$への移動に注目します.

\begin{eqnarray} y_B &=& B x_B \nonumber \\ Q^{-1} y_A &=& BP^{-1}x_A \quad (y_A = Q y_B, x_A = P x_B なので) \nonumber \\ y_A &=& Q B P^{-1} x_A \nonumber \end{eqnarray}

また, $y_A = A x_A$より,

\begin{eqnarray} A &=& Q B P^{-1} \nonumber \\ B &=& Q^{-1} A P \nonumber \end{eqnarray}

以上.

「https://contentsviewer.work/Master/Math/LinearAlgebra/TransAndRep/TransAndRep」から取得

図で理解する変換行列と表現行列

ベクトル空間

数ベクトル空間

線形写像

座標

基底の変換行列

表現行列

全体像

諸定理

関連